What is the difference between wavelet transform and Fourier transform? Which is better for wavelet transform and Fourier transform? We analyze through the detailed interpretation of wavelet transform and Fourier transform, the difference between wavelet transform and Fourier transform, and the shortcomings of Fourier transform.
The difference between wavelet transform and Fourier transformIn Fourier analysis, signals are represented as a function of a single variable (time or frequency), so time domain frequency domain analysis cannot be performed simultaneously.
In wavelet analysis, the joint time-scale function is used to analyze the signal, and the wavelet base is constructed by translation and expansion. Since the wavelet has the characteristics of time shift and multi-scale resolution, time-frequency domain analysis can be performed simultaneously.


As shown above, the topmost is the stationary signal whose frequency is always constant. The lower two are non-stationary signals whose frequency changes with time, and they also contain four components of the same frequency as the uppermost signal. After doing the FFT, we found that the signals in the three time domains have huge differences, and the spectrum (amplitude spectrum) is very consistent. Especially for the two non-stationary signals below, we can't distinguish them from the spectrum, because the components of the four frequencies they contain are exactly the same, but the order of appearance is different.
It can be seen that the Fourier transform has a natural defect in dealing with non-stationary letters. It can only get the components of a frequency that the whole message contains, but it is unknown to the moment when each component appears. Therefore, the two signals with very different time domains may be the same as the spectrum.
Detailed analysis of wavelet transform and Fourier transformFrom Fourier transform to wavelet transform, it is not a completely abstract thing, it can be very vivid. Wavelet transform has a clear physical meaning. If we look at the problems it faces when it comes up, we can sort out very clear ideas.
In the following, according to the order of Fourier--"short-time Fourier transform--" wavelet transform, let me talk about why there is a wavelet thing and how the wavelet is.
First, Fourier transformThe basic concept of the Fourier transform is not repeated here. By default, everyone is now on the road to understand Fourier but still not understanding the wavelet.
Below we mainly lack the Fourier transform. That is, we know that the Fourier transform can analyze the spectrum of the signal, so why should we propose a wavelet transform? The answer is "the Fourier transform has limitations for non-stationary processes." Look at the following simple signal:
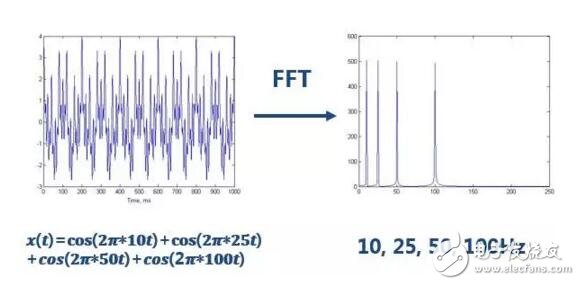
After completing the FFT (Fast Fourier Transform), you can see a clear four lines on the spectrum, the signal contains four frequency components.
Everything is fine. But what if it is a non-stationary signal whose frequency changes with time?
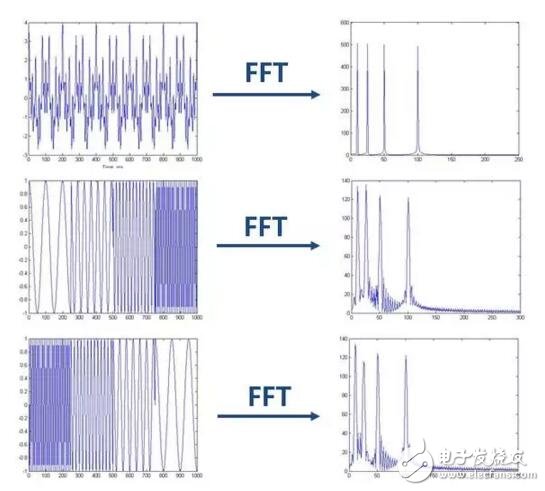
As shown above, the topmost is the stationary signal whose frequency is always constant. The lower two are non-stationary signals whose frequency changes with time, and they also contain four components of the same frequency as the uppermost signal. After doing the FFT, we found that the signals in the three time domains have huge differences, and the spectrum (amplitude spectrum) is very consistent. Especially for the two non-stationary signals below, we can't distinguish them from the spectrum, because the components of the four frequencies they contain are exactly the same, but the order of appearance is different.
It can be seen that the Fourier transform has a natural defect in processing non-stationary signals. It can only get the components of a frequency that the signal generally contains, but it is unknown to the moment when each component appears. Therefore, the two signals with very different time domains may be the same as the spectrum.
However, most of the stationary signals are artificially produced. A large number of signals in nature are almost non-stationary. Therefore, in papers such as biomedical signal analysis, the naive method of simple Fourier transform is basically invisible.
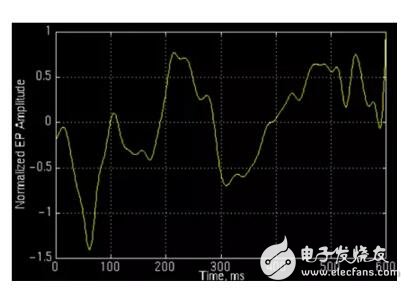
The figure above shows the event-related potential of a normal person. For such non-stationary signals, it is not enough to know which frequency components are included. We also want to know when each component appears. Know the frequency of the signal as a function of time, the instantaneous frequency and its amplitude at each moment - this is the time-frequency analysis.
Second, Short-Time Fourier Transform (STFT)A simple and feasible way is to add windows. “The whole time domain process is decomposed into a number of small processes of equal length. Each small process is approximately stationary, and then Fourier transform, we know at what time point what frequency appears.†This is the short-time Fourier Transform.
Look at the picture:
Do the FFT in the time domain divided into segments, do you know the frequency components change over time?
In this way, you can get a time-frequency diagram of a signal:

You can see the four frequency range components of 10Hz, 25 Hz, 50 Hz, and 100 Hz, and you can see the time of appearance. The two rows of peaks are symmetrical, so you only have to look at one row.
Is it great? Time-frequency analysis results are at hand. But STFT is still flawed.
There is a problem with STFT. How wide should we use window functions?
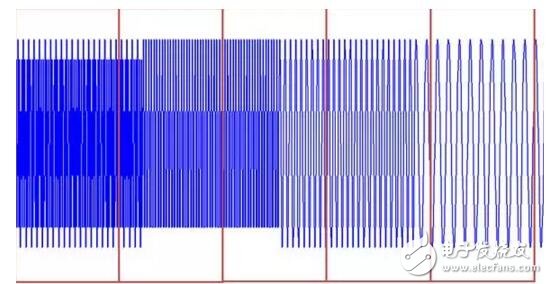
The window is too wide and too narrow to have problems:
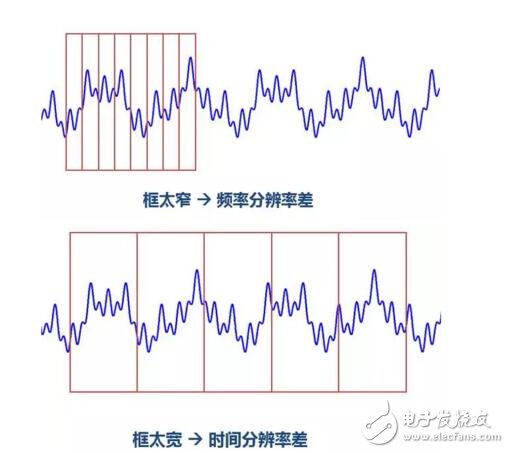
The window is too narrow, and the signal in the window is too short, which will result in inaccurate frequency analysis and poor frequency resolution. The window is too wide, the time domain is not fine enough, and the time resolution is low.
(Insert here, this principle can be explained by the Heisenberg uncertainty principle. Similar to the fact that we can't simultaneously acquire the momentum and position of a particle, we can't get the exact time and frequency of the signal at the same time. There is a contradiction. We don't know which frequency component exists at a certain moment. We only know that the component of a certain frequency band exists in a time period. Therefore, the instantaneous frequency of absolute meaning does not exist.)
Take a look at the example effect:
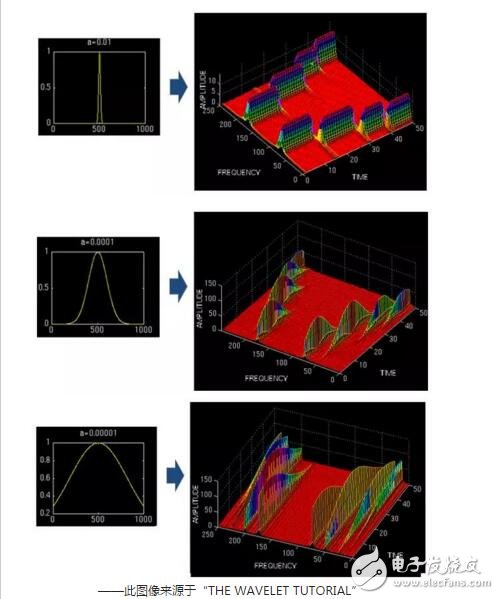
In the above figure, the same signal (four frequency components) is used as a STFT with windows of different widths. The result is shown in the right figure. With a narrow window, the time-frequency diagram has a high resolution on the time axis, with several peaks being substantially rectangular, and a wide window becoming a stretch of low mountains. However, on the frequency axis, the narrow window is obviously not as accurate as the two wide windows below.
Therefore, the narrow window has high time resolution, low frequency resolution, low wide window time resolution and high frequency resolution. For time-varying, non-stationary signals, the high frequency is suitable for small windows and the low frequency is suitable for large windows. However, the window of the STFT is fixed, and the width does not change in one STFT, so the STFT still cannot meet the frequency of the unsteady signal change.
Third, wavelet transformThen you might think of changing the size of the window. Do you have to do STFT a few times? ! That's right, the wavelet transform has this idea.
But in fact, wavelets don't do this (some people think that "wavelet transform is based on algorithm, plus unequal window, Fourier transform for each small part", which is not accurate. Wavelet transform does not use windows The idea is not to do the Fourier transform.)
As for why you don't use a variable-window STFT, I think it's because the redundancy is too serious, and STFT can't do orthogonalization, which is also a major flaw.
So the starting point of the wavelet transform is different from the STFT. The STFT is to window the signal and segment the FFT; the wavelet directly replaces the base of the Fourier transform - replacing the infinitely long trigonometric base with a finitely long decaying wavelet base. This will not only get the frequency, but also the time~
ã€Explanation】
Let's review the Fourier transform. If you don't know why the Fourier transform can get the various frequency components of the signal, you can borrow my picture to understand.
The Fourier transform uses an infinitely long trigonometric function as the basis function:

This base function will scale and translate (in fact, the decomposition of two orthogonal bases). The narrowing is narrow, corresponding to the high frequency; the width is wide, corresponding to the low frequency. This basis function is then multiplied by the signal. The result of multiplying a certain scale (width and width) can be understood as the number of frequency components corresponding to the current scale contained in the signal. Thus, the basis function will multiply the signal at some scale to get a large value, because there is a coincidence relationship between the two. Then we know how much the signal contains the components of that frequency.
A closer look reveals that this step is actually calculating the correlation between the signal and the trigonometric function.
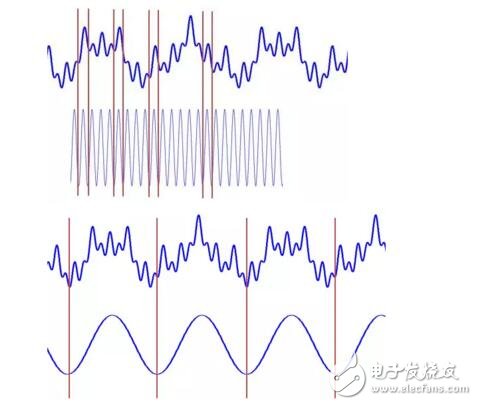
Look, these two scales can be multiplied by a large value (high correlation), so the signal contains more of these two frequency components, and two peaks appear in the two frequencies in the spectrum.
The above is the principle of the Fourier transform in the shallow sense.
As mentioned earlier, the change in wavelets is to replace the infinitely long trigonometric base with a finitely long decaying wavelet base.
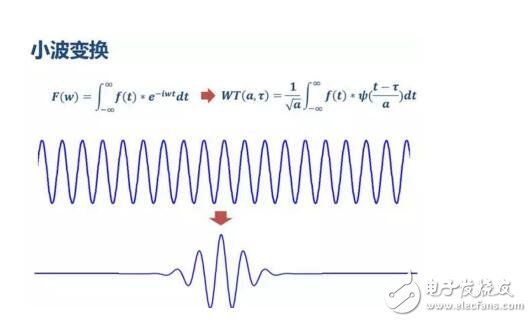
This is why it is called "wavelet" because it is a small wave~
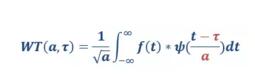
It can be seen from the formula that unlike the Fourier transform, the variable has only the frequency ω, and the wavelet transform has two variables: the scale a (scale) and the translation τ (translaTIon). The scale a controls the expansion and contraction of the wavelet function, and the translation amount τ controls the translation of the wavelet function. The scale corresponds to the frequency (inverse ratio), and the amount of translation τ corresponds to time.

When scaling and panning to such a coincidence, they are multiplied to get a large value. This time, unlike the Fourier transform, this not only knows the signal has a component of this frequency, but also knows where it exists in the time domain.
And when we multiply and multiply the signal at each scale, we know which frequency components the signal contains at each location.
see it? With the wavelet, we are no longer afraid of the unstable signal! From now on, you can do time-frequency analysis!
Doing a Fourier transform can only get one spectrum, but doing a wavelet transform can get a time spectrum!
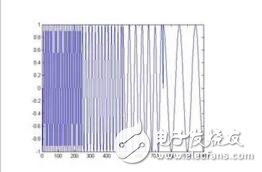
↑: time domain signal
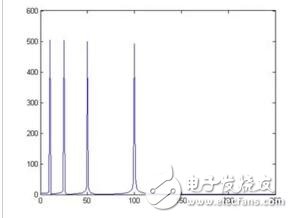
↑: Fourier transform results
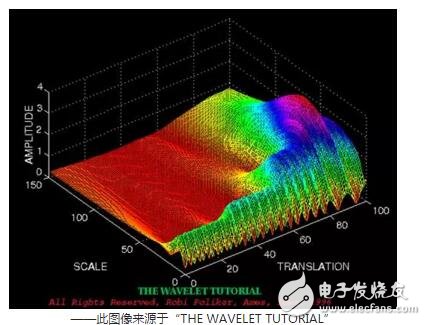
↑: wavelet transform results
Wavelets have some advantages:
1. We know that for the mutated signal, the Fourier transform has the Gibbs effect, and we use the infinitely long trigonometric function to fit the bad mutation signal:
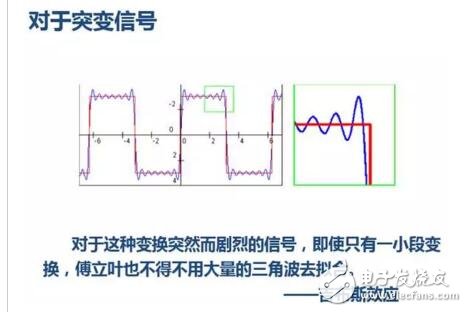
However, the attenuated wavelet is different:
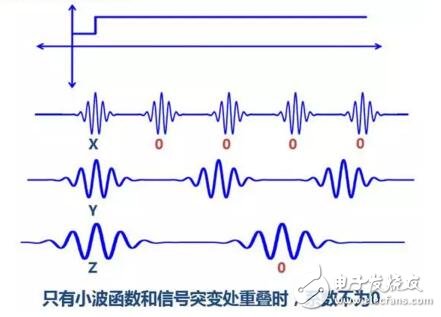
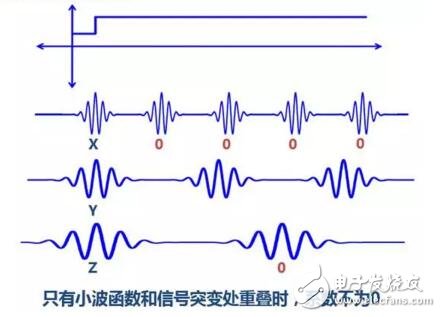
2. The wavelet can be orthogonalized, and the short-time Fourier transform cannot.
For Sony:
For Xperia Z4V, For Xperia Z3V
For Google:
For Nexus 4, For Nexus 5, For Nexus 6, For Nexus 7
For MOTORALA:
For Moto Droid Turbo, For Moto Droid Turbo 2, For Moto Droid 5
For NOKIA:
For Lumia 920, For Lumia 928, For Nokia Lumia 93, For Lumia 950, For Lumia 950 XL, For Lumia 1020, For Nokia Lumia 1050, For Nokia Lumia 822, For Nokia Lumia 735
For HTC:
For HTC ONE MAX T6, For HTC Incredible 4G, For HTC ONE mini 2, For HTC Droid DNA
For LG:
For LG Nexus 4, For LG Nexus 5, For LG G Pro, For LG D1L, For LG LTE2
For Iphone:
For Iphone8/X/XR/XS Max
Compabile Models:
For Samsung:
For Galaxy S6, For Galaxy S6 Edge, For Galaxy S6 Edge+,
For Galaxy S6 Active, For Galaxy S6 Duos, For Galaxy Note Edge,
For Galaxy S7, For Galaxy S7 Edge, For Galaxy Note 5
For Galaxy S8, For Galaxy S8 Plus, For Galaxy Note 8
For Galaxy S9,For Galaxy S9 Plus
For Others:
Guangzhou HangDeng Tech Co. Ltd , http://www.hangdengtech.com